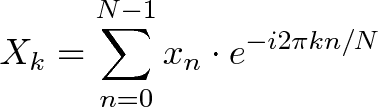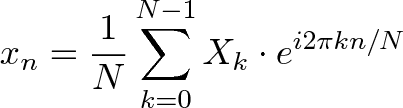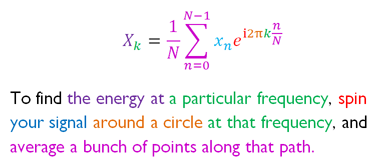Read this in other languages: english.
La transformation de Fourier (ℱ) est une opération qui transforme une fonction intégrable sur ℝ en une autre fonction, décrivant le spectre fréquentiel de cette dernière
La Transformée de Fourier Discrète (TFD) convertit une séquence finie d'échantillons également espacés d'une fonction, dans une séquence de même longueur d'échantillons, également espacés de la Transformée de Fourier à temps discret (TFtd), qui est une fonction complexe de la fréquence. L'intervalle auquel le TFtd est échantillonné est l'inverse de la durée de la séquence d'entrée. Une TFD inverse est une série de Fourier, utilisant les échantillons TFtd comme coefficients de sinusoïdes complexes aux fréquences TFtd correspondantes. Elle a les mêmes valeurs d'échantillonnage que la séquence d'entrée originale. On dit donc que la TFD est une représentation du domaine fréquentiel de la séquence d'entrée d'origine. Si la séquence d'origine couvre toutes les valeurs non nulles d'une fonction, sa TFtd est continue (et périodique), et la TFD fournit les échantillons discrets d'une fenêtre. Si la séquence d'origine est un cycle d'une fonction périodique, la TFD fournit toutes les valeurs non nulles d'une fenêtre TFtd.
Transformée de Fourier Discrète converti une séquence de N nombres complexes:
{xn} = x0, x1, x2 ..., xN-1
en une atre séquence de nombres complexes::
{Xk} = X0, X1, X2 ..., XN-1
décrite par:
The Transformée de Fourier à temps discret (TFtd) est une forme d'analyse de Fourier qui s'applique aux échantillons uniformément espacés d'une fonction continue. Le terme "temps discret" fait référence au fait que la transformée fonctionne sur des données discrètes (échantillons) dont l'intervalle a souvent des unités de temps. À partir des seuls échantillons, elle produit une fonction de fréquence qui est une somme périodique de la Transformée de Fourier continue de la fonction continue d'origine.
A Transformation de Fourier rapide (FFT pour Fast Fourier Transform) est un algorithme de calcul de la transformation de Fourier discrète (TFD). Il est couramment utilisé en traitement numérique du signal pour transformer des données discrètes du domaine temporel dans le domaine fréquentiel, en particulier dans les oscilloscopes numériques (les analyseurs de spectre utilisant plutôt des filtres analogiques, plus précis). Son efficacité permet de réaliser des filtrages en modifiant le spectre et en utilisant la transformation inverse (filtre à réponse impulsionnelle finie).
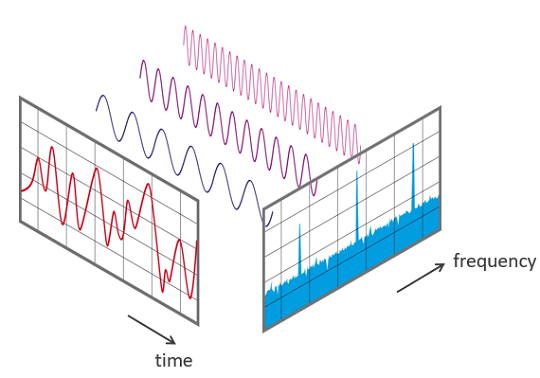
Cette transformation peut être illustée par la formule suivante. Sur la période de temps mesurée dans le diagramme, le signal contient 3 fréquences dominantes distinctes.
Vue d'un signal dans le domaine temporel et fréquentiel:
An FFT algorithm computes the discrete Fourier transform (DFT) of a sequence, or its inverse (IFFT). Fourier analysis converts a signal from its original domain to a representation in the frequency domain and vice versa. An FFT rapidly computes such transformations by factorizing the DFT matrix into a product of sparse (mostly zero) factors. As a result, it manages to reduce the complexity of computing the DFT from O(n2), which arises if one simply applies the definition of DFT, to O(n log n), where n is the data size.
Un algorithme FFT calcule la Transformée de Fourier discrète (TFD) d'une séquence, ou son inverse (IFFT). L'analyse de Fourier convertit un signal de son domaine d'origine en une représentation dans le domaine fréquentiel et vice versa. Une FFT calcule rapidement ces transformations en factorisant la matrice TFD en un produit de facteurs dispersés (généralement nuls). En conséquence, il parvient à réduire la complexité de calcul de la TFD de O (n 2 ), qui survient si l'on applique simplement la définition de TFD, à O (n log n), où n est la taille des données.
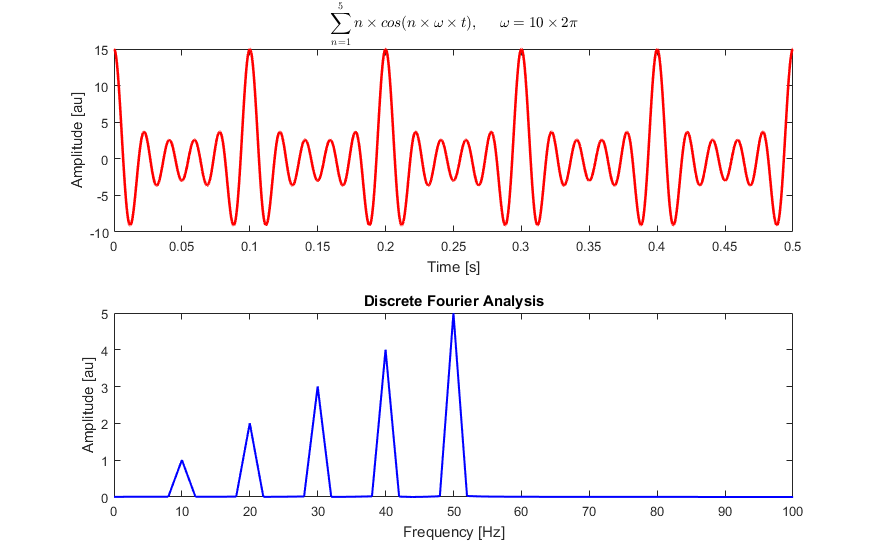
Voici une analyse de Fourier discrète d'une somme d'ondes cosinus à 10, 20, 30, 40, et 50 Hz:
La Transformée de Fourier est l'une des connaissances les plus importante jamais découverte. Malheureusement, le son sens est enfoui dans des équations denses::
et
Plutôt que se noyer dans les symboles, faisons en premier lieu l'expérience de l'idée principale. Voici une métaphore en français simple:
- Que fait la transformée de Fourier ? A partir d'un smoothie, elle trouve sa recette.
- Comment ? Elle passe le smoothie dans un filtre pour en extraire chaque ingrédient.
- Pourquoi ? Les recettes sont plus faciles à analyser, comparer et modifier que le smoothie lui-même.
- Comment récupérer le smoothie ? Re-mélanger les ingrédients.
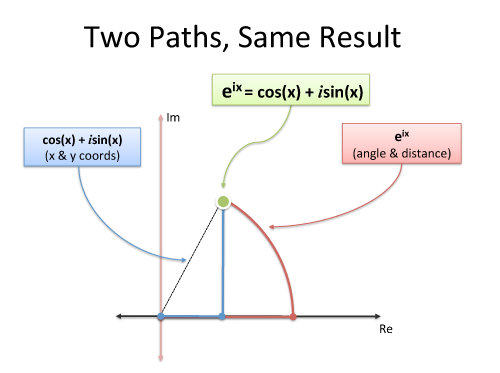
Pensez en cercles, pas seulement en sinusoïdes
La transformée de Fourier concerne des trajectoires circulaires (pas les sinusoïdes 1-d) et la formuled'Euler est une manière intelligente d'en générer une:
Doit-on utiliser des exposants imaginaires pour se déplacer en cercle ? Non. Mais c'est pratique et compact. Et bien sûr, nous pouvons décrire notre chemin comme un mouvement coordonné en deux dimensions (réelle et imaginaire), mais n'oubliez pas la vue d'ensemble: nous sommes juste en déplacement dans un cercle.
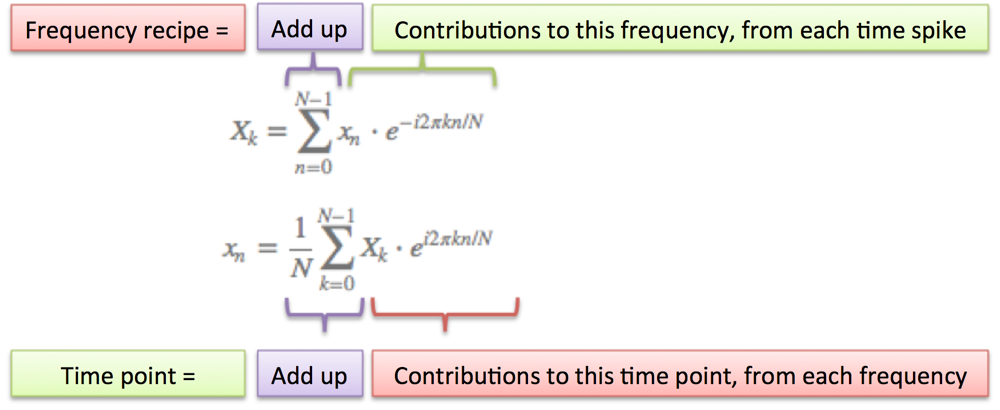
À la découverte de la transformation complète
L'idée générale: notre signal n'est qu'un tas de pics de temps, d'instant T ! Si nous combinons les recettes pour chaque pic de temps, nous devrions obtenir la recette du signal complet.
La transformée de Fourier construit cette recette fréquence par fréquence:
Quelques notes
- N = nombre d'échantillons de temps dont nous disposons
- n = échantillon actuellement étudié (0 ... N-1)
- xn = valeur du signal au temps n
- k = fréquence actuellement étudiée (0 Hertz up to N-1 Hertz)
- Xk = quantité de fréquence k dans le signal (amplitude et phase, un nombre complexe)
- Le facteur 1 / N est généralement déplacé vers la transformée inverse (passant des fréquences au temps). Ceci est autorisé, bien que je préfère 1 / N dans la transformation directe car cela donne les tailles réelles des pics de temps. Vous pouvez être plus ambitieux et utiliser 1 / racine carrée de (N) sur les deux transformations (aller en avant et en arrière crée le facteur 1 / N).
- n/N est le pourcentage du temps que nous avons passé. 2 _ pi _ k est notre vitesse en radians/s. e ^ -ix est notre chemin circulaire vers l'arrière. La combinaison est la distance parcourue, pour cette vitesse et ce temps.
- Les équations brutes de la transformée de Fourier consiste simplement à "ajouter les nombres complexes". De nombreux langages de programmation ne peuvent pas gérer directement les nombres complexes, on converti donc tout en coordonnées rectangulaires, pour les ajouter.
Stuart Riffle a une excellente interprétation de la transformée de Fourier: