Simulator for quantum networks and channels

The Simulator for Quantum Networks and Channels (SQUANCH) is an open-source Python library for creating parallelized simulations of distributed quantum information processing. The framework includes many features of a general-purpose quantum computing simulator, but it is optimized specifically for simulating quantum networks. It includes functionality to allow users to easily design complex multi-party quantum networks, extensible classes for modeling noisy quantum channels, and a multiprocessed NumPy backend for performant simulations.

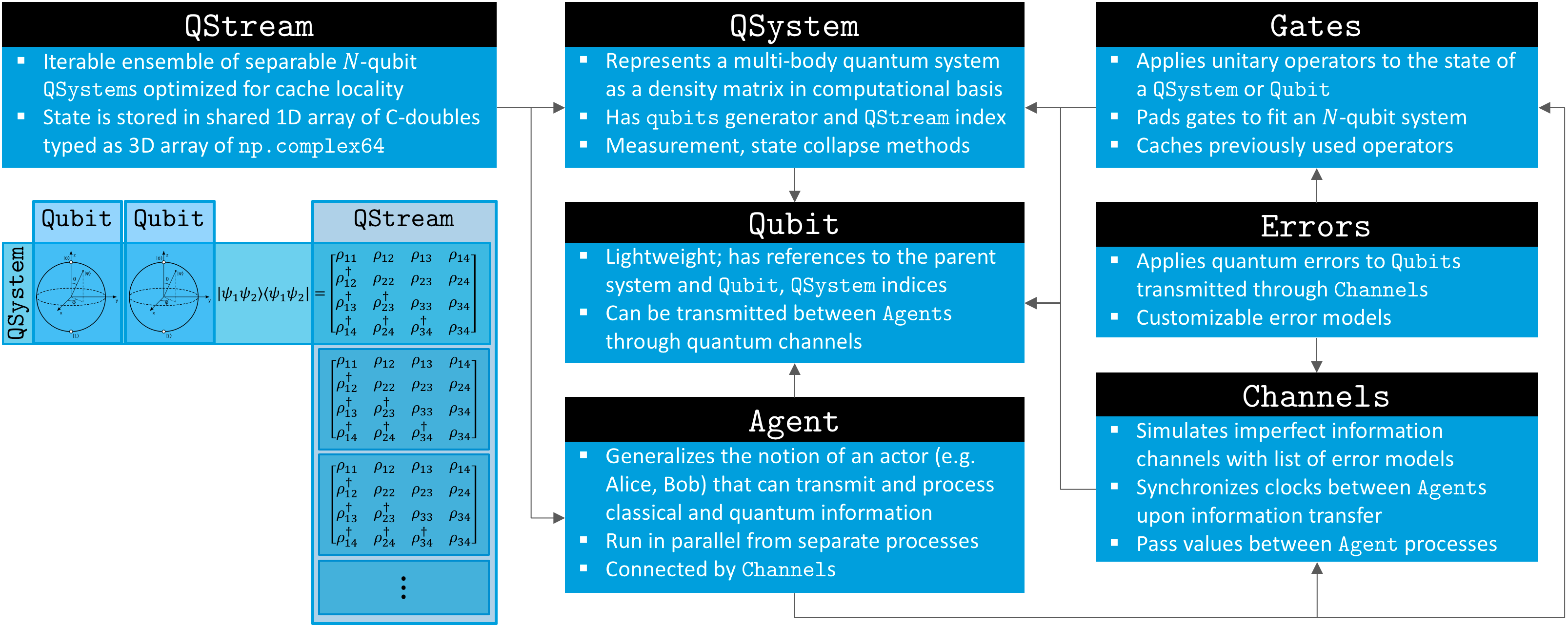
A schematic overview of the modules available in SQUANCH is shown below. (Refer to the documentation or the whitepaper for more details.)

SQUANCH is developed as part of the Intelligent Quantum Networks and Technologies (INQNET) program, a collaboration between AT&T and the California Institute of Technology.

Documentation

Documentation for this package is available at the documentation website or as a pdf manual. We encourage interested users to read the whitepaper for the SQUANCH platform, "A distributed simulation framework for quantum networks and channels" (arXiv: 1808.07047), which provides an overview of the framework and a primer on quantum information.

Installation

You can install SQUANCH directly using the Python package manager, pip:

pip install squanch

If you don't have pip, you can get it using easy_install pip.

Demonstrations

Demonstrations of various quantum protocols can be found in the demos folder and in the documentation:

• Quantum teleportation
• Superdense coding
• Man-in-the-middle attack
• Quantum error correction

Example: quantum interception attack

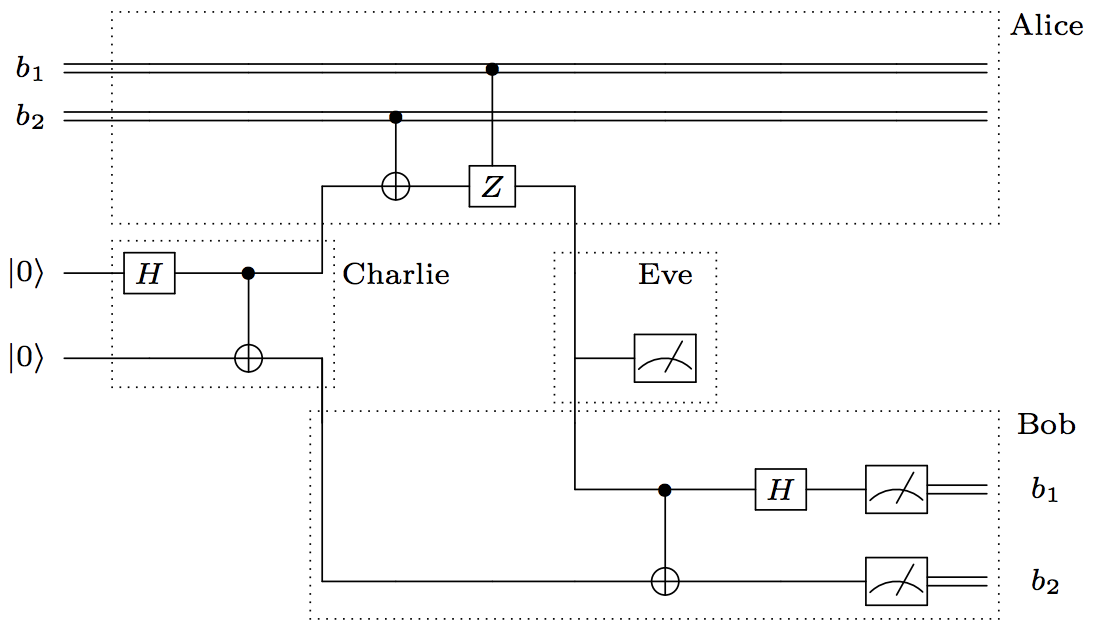
As an example to put in this readme, let's consider a scenario where Alice wants to send data to Bob. For security, she transmits her message through quantum superdense coding. In this scenario, shown below as a circuit diagram, we have four Agents, who act as follows:

• Charlie generates entangled pairs of qubits, which he sends to Alice and Bob.
• Alice receives Charlie's qubit. She encodes two bits of her data in it and sends it Bob.
• Bob receives the qubits from Charlie and Alice. He operates jointly on them and measures them to reconstruct Alice's two bits of information.
• However, the fourth agent, Eve, wants to know Alice's data. She intercepts every qubit Alice sends to Bob, measures it, and re-transmits it to Bob, hoping he won't notice.

An implementation of this scenario in SQUANCH is given below.

import numpy as np
import matplotlib.image as image
from squanch import *

class Charlie(Agent):
    '''Charlie sends Bell pairs to Alice and Bob'''
    def run(self):
        for qsys in self.qstream:
            a, b = qsys.qubits
            H(a)
            CNOT(a, b)
            self.qsend(alice, a)
            self.qsend(bob, b)
            
class Alice(Agent):
    '''Alice tries to send data to Bob, but Eve intercepts'''
    def run(self):
        for _ in self.qstream:
            bit1 = self.data.pop(0)
            bit2 = self.data.pop(0)
            q = self.qrecv(charlie)
            if bit2 == 1: X(q)
            if bit1 == 1: Z(q)
            # Alice unknowingly sends the qubit to Eve
            self.qsend(eve, q) 
            
class Eve(Agent):
    '''Eve naively tries to intercept Alice's data'''
    def run(self):
        bits = [] 
        for _ in self.qstream:
            a = self.qrecv(alice)
            bits.append(a.measure())
            self.qsend(bob, a)
        self.output(bits)
            
class Bob(Agent):
    '''Bob receives Eve's intercepted data'''
    def run(self):
        bits = []
        for _ in self.qstream:
            a = self.qrecv(eve)
            c = self.qrecv(charlie)
            CNOT(a, c)
            H(a)
            bits.extend([a.measure(), c.measure()])
        self.output(bits)
    
# Load Alice's data (an image) and serialize it to a bitstream
img = image.imread("docs/source/img/foundryLogo.bmp") 
bitstream = list(np.unpackbits(img))

# Prepare an appropriately sized quantum stream
qstream = QStream(2, int(len(bitstream) / 2))
out = Agent.shared_output()

# Instantiate agents
alice = Alice(qstream, out, data=bitstream)
bob = Bob(qstream, out)
charlie = Charlie(qstream, out)
eve = Eve(qstream, out)

# Connect the agents to form the network
alice.qconnect(bob)
alice.qconnect(eve)
alice.qconnect(charlie)
bob.qconnect(charlie)
bob.qconnect(eve)

# Run the simulation
Simulation(alice, eve, bob, charlie).run()

# Display the images Alice sent, Eve intercepted, and Bob received
# (Plotting code omitted for brevity; results shown below)

Citation

If you are doing research using SQUANCH, please cite our whitepaper:

B. Bartlett, "A distributed simulation framework for quantum networks and channels," arXiv: 1808.07047 [quant-ph], Aug. 2018.