Welcome to this repository! Since you are here, I am assuming that Computer Arithmetic is of interest to you (i.e. the art and science of using transistors to do computations, in silicone).
Moreover, I am guessing that you are just as fascinated (as I am) with the paper-and-pencil digital equivalent of of doing division and (not so often taught nowadays) the square root. This family of algorithms is formally known as the digit-recurrence family of algorithms.
In my M.Sc. thesis, entitled "Incorporating Multiplication Into Digit-Recurrence Division and the Square Root to Calculate
(a*b)/c/sqrt(a*b)" (linked here), I have delved into the derivation
and the hardware implementation of a fused multiplier and a square rooting unit (just in case, you thought
having a such a machine instruction would change your life, obviously I did!).
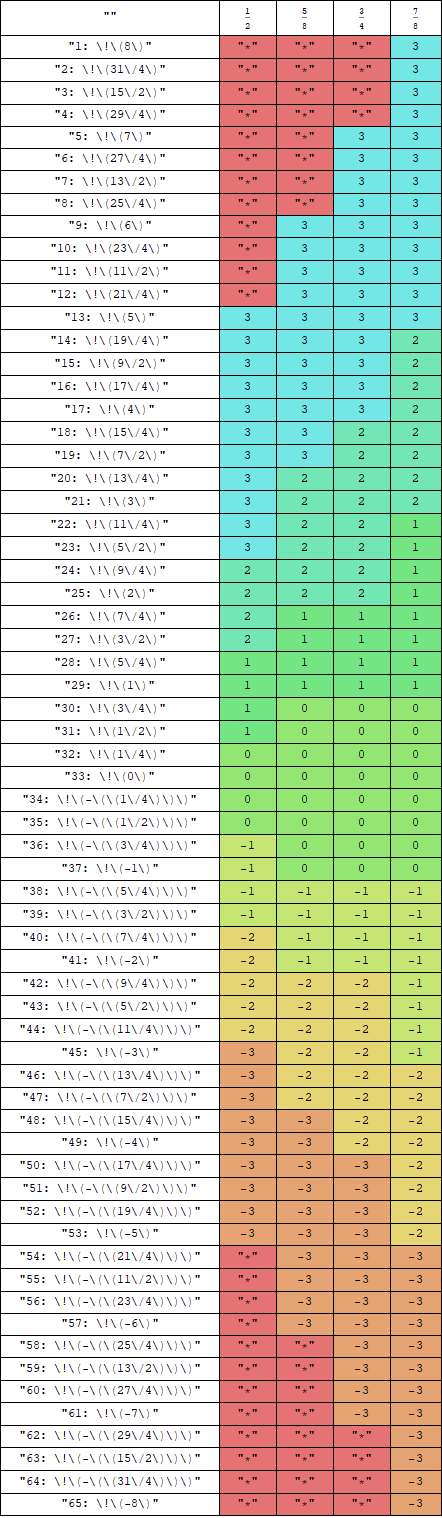
Any such unit, while based on the digit-recurrence family of algorithms, need a "guessing table", usually stored within a ROM (read-only memory) on-board. This ROM is formally called the "SRT table".
Basically, this so-called SRT Table serves the same purpose "trial and error" serve when dividing on paper, and it looks something like this below:
In fact, this very SRT table has been generated by the three Mathematica notebooks of this repository, namely:
- System Parameters Module Supporting Higher-Order Digit Selectors
- Designer Cell Supporting Higher-Order Digit Selectors
- Lookup Table Generator Supporting Higher-Order Digit Selectors
It is very simple, the first thing you need to do is to install Mathematica 8.0 or later. Then open the notebooks and execute them in the same order shown in the numbered list of the previous section.
As the name suggests, this is where you make the decisions most crucial to the design of your hardware unit, the most important of which is "bits per high-radix digit" which is a lengthy way of describing the number of bits to be consumed by your digital circuit in every iteration (i.e. with every tick of the digital clock).
The higher this number is, the faster your circuit is going to be.
However, this is going to be at the expense of the complexity of the hardware needed (both in terms of the number of logic gates as well as in terms of the ROM size required to store the SRT table).
"2" is considered a good choice for a practically-sized unit.
Here, you apply the different optimizations needed to achieve a table of a practical size. Once applied, the "constants table" is automatically updated which is all what is needed to generate the actual contents of the SRT table.
The table contents are generated by this notebook, along with a C code fragment that permits simulating the hardware unit using the simulator, which is a part of the same repositry (written in the C programming language).
Note that to display the table in colors, you will have to click a checkbox that shows in the notebook.
As far as I know, there is no software currently available in the public domain that permits generating the contents of the SRT table used within of a Digit-Recurrence Divider/Square-Rooting unit that is as powerful, and rigorously verified as this one.
I hope that by using it that you will get to admire the beauty of this class of algorithms as much as I did, and that you will go over the way I explain them in the first part of my thesis.
For any questions or inqueries, please do not hesitate to get in touch with me.
last updated by Orwa Diraneyya on 16th of April, 2019